14. SGD 解决方案
这是我对上个练习的解决方案
def sgd_update(trainables, learning_rate=1e-2):
"""
Updates the value of each trainable with SGD.
Arguments:
`trainables`: A list of `Input` nodes representing weights/biases.
`learning_rate`: The learning rate.
"""
# Performs SGD
#
# Loop over the trainables
for t in trainables:
# Change the trainable's value by subtracting the learning rate
# multiplied by the partial of the cost with respect to this
# trainable.
partial = t.gradients[t]
t.value -= learning_rate * partial我们来看下最后几行:
# Performs SGD
#
# Loop over the trainables
for t in trainables:
# Change the trainable's value by subtracting the learning rate
# multiplied by the partial of the cost with respect to this
# trainable.
partial = t.gradients[t]
t.value -= learning_rate * partial有两个关键步骤。第一步,Cost (C) 关于 trainable t 的偏导 可以如下得到
partial = t.gradients[t]第二步,trainable 的值根据等式 (12) 进行更新
t.value -= learning_rate * partial对所有 trainable 执行。
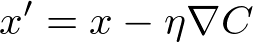
等式 (12)
这样的话,下次在网络中传递时,损失会下降。
我在下面又提供了同一道测验。如果你尚未练习的话,请将迭代次数设为 1000,看看损失是否下降了!
Start Quiz: