06. 学习和损失

学习和损失

就像当前状态的 MiniFlow 一样，神经网络传入输入并产生输出。但是与当前状态的 MiniFlow 不一样，神经网络可以逐渐改善其输出的准确性（很难想象 Add 会逐渐提高准确性！）。要理解为何准确性很重要，请首先实现一个比 Add 更难（也更实用）的节点。

线性方程

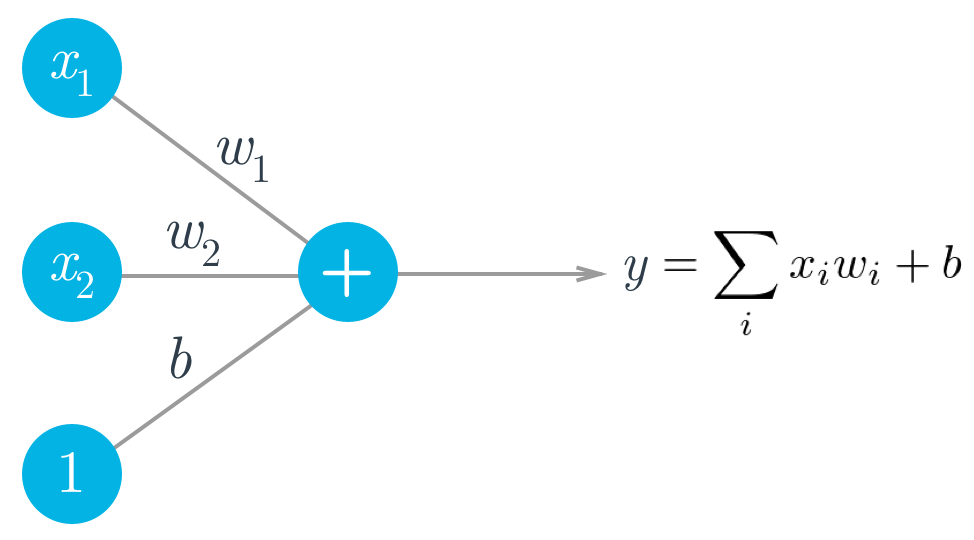
回忆下神经网络入门那部分课程。简单的人工神经元取决于以下三个组件：

  • 输入， x_i
  • 权重， w_i
  • 偏置， b

输出 y 就是输入加上偏置的加权和。

注意，通过更改权重，你可以更改任何给定输入对输出带来的影响。神经网络的学习流程发生在反向传播过程中。在反向传播中，网络会修改权重，以改善网络的输出准确性。你很快将应用所有这些知识。

在下个测验中，你将构建一个线性神经元，该神经元通过应用简化的加权和生成输出。Linear 应该传入长为 n 的传入节点列表、长度为 n 的权重列表和偏置。

说明

  1. 打开下面的 nn.py。通读该神经网络，看看 Linear 的预期输出结果。
  2. 打开下面的 miniflow.py。修改 Linear（Node 的子类）以生成一个输出： y = \sum w_i x_i + b。

（提示，你可以使用 numpy 解答这道测验，但是也可以直接通过 Python 解答。）

Start Quiz:

"""
NOTE: Here we're using an Input node for more than a scalar.
In the case of weights and inputs the value of the Input node is
actually a python list!

In general, there's no restriction on the values that can be passed to an Input node.
"""
from miniflow import *

inputs, weights, bias = Input(), Input(), Input()

f = Linear(inputs, weights, bias)

feed_dict = {
    inputs: [6, 14, 3],
    weights: [0.5, 0.25, 1.4],
    bias: 2
}

graph = topological_sort(feed_dict)
output = forward_pass(f, graph)

print(output) # should be 12.7 with this example
"""
Write the Linear#forward method below!
"""


class Node:
    def __init__(self, inbound_nodes=[]):
        # Nodes from which this Node receives values
        self.inbound_nodes = inbound_nodes
        # Nodes to which this Node passes values
        self.outbound_nodes = []
        # A calculated value
        self.value = None
        # Add this node as an outbound node on its inputs.
        for n in self.inbound_nodes:
            n.outbound_nodes.append(self)

    # These will be implemented in a subclass.
    def forward(self):
        """
        Forward propagation.

        Compute the output value based on `inbound_nodes` and
        store the result in self.value.
        """
        raise NotImplemented


class Input(Node):
    def __init__(self):
        # An Input Node has no inbound nodes,
        # so no need to pass anything to the Node instantiator
        Node.__init__(self)

        # NOTE: Input Node is the only Node where the value
        # may be passed as an argument to forward().
        #
        # All other Node implementations should get the value
        # of the previous nodes from self.inbound_nodes
        #
        # Example:
        # val0 = self.inbound_nodes[0].value
    def forward(self, value=None):
        # Overwrite the value if one is passed in.
        if value is not None:
            self.value = value


class Linear(Node):
    def __init__(self, inputs, weights, bias):
        Node.__init__(self, [inputs, weights, bias])

        # NOTE: The weights and bias properties here are not
        # numbers, but rather references to other nodes.
        # The weight and bias values are stored within the
        # respective nodes.

    def forward(self):
        """
        Set self.value to the value of the linear function output.

        Your code goes here!
        """
        pass



def topological_sort(feed_dict):
    """
    Sort the nodes in topological order using Kahn's Algorithm.

    `feed_dict`: A dictionary where the key is a `Input` Node and the value is the respective value feed to that Node.

    Returns a list of sorted nodes.
    """

    input_nodes = [n for n in feed_dict.keys()]

    G = {}
    nodes = [n for n in input_nodes]
    while len(nodes) > 0:
        n = nodes.pop(0)
        if n not in G:
            G[n] = {'in': set(), 'out': set()}
        for m in n.outbound_nodes:
            if m not in G:
                G[m] = {'in': set(), 'out': set()}
            G[n]['out'].add(m)
            G[m]['in'].add(n)
            nodes.append(m)

    L = []
    S = set(input_nodes)
    while len(S) > 0:
        n = S.pop()

        if isinstance(n, Input):
            n.value = feed_dict[n]

        L.append(n)
        for m in n.outbound_nodes:
            G[n]['out'].remove(m)
            G[m]['in'].remove(n)
            # if no other incoming edges add to S
            if len(G[m]['in']) == 0:
                S.add(m)
    return L


def forward_pass(output_node, sorted_nodes):
    """
    Performs a forward pass through a list of sorted nodes.

    Arguments:

        `output_node`: A node in the graph, should be the output node (have no outgoing edges).
        `sorted_nodes`: A topologically sorted list of nodes.

    Returns the output Node's value
    """

    for n in sorted_nodes:
        n.forward()

    return output_node.value

Next Concept