19. MC 控制:常量 α(第 2 部分)
MC 控制:常量 α
在之前的练习(练习:增量均值)中,你完成了一种算法,该算法可以不断估算一系列数字 (x_1, x_2, \ldots, x_n) 的均值。running_mean 会接受一系列数字 x 作为输入并返回一个 mean_values 列表,其中 mean_values[k] 是 x[:k+1] 的均值。
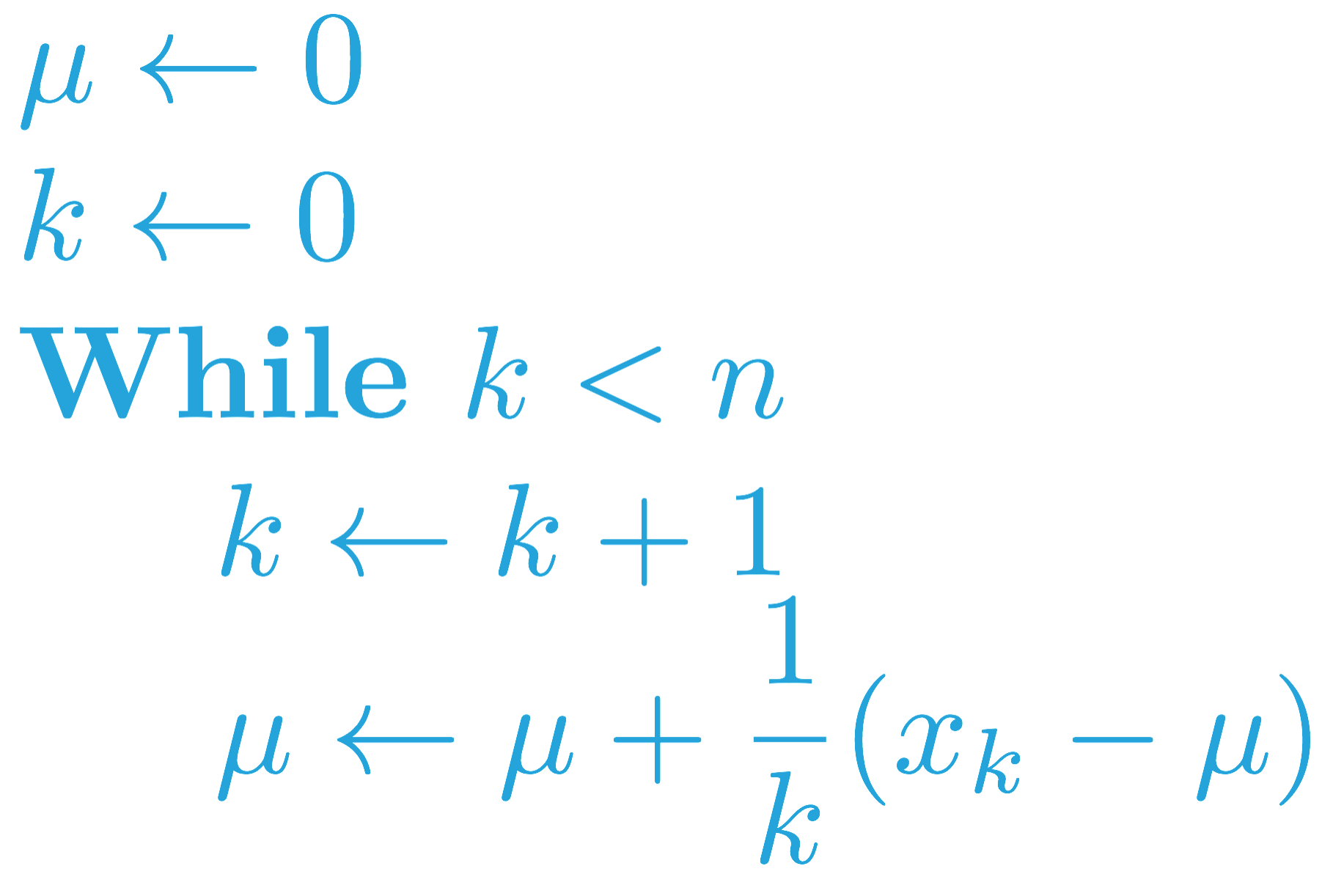
当我们在下个部分(MC 控制:策略评估)针对蒙特卡洛控制调整该算法时,序列 (x_1, x_2, \ldots, x_n) 对应的是经历相同状态动作对后获得的回报。
但是,(相同状态动作对)的抽样回报可能对应于很多不同的策略。因为控制算法是由一系列的评估和改进步骤组成,在每个互动阶段后,策略被改进。尤其是,我们提到后续时间步抽取的回报很可能对应的策略更优化。
因此,有必要修改策略评估步骤并改为使用常量步长,我们在上个视频(MC 控制:常量 α(第 1 部分))中表示为 \alpha。这样会确保智能体在估算动作值时主要考虑最近抽样的回报,并逐渐忘记很久之前的回报。
你可以在下方找到类似的伪代码(对一系列 (x_1, x_2, \ldots, x_n) 采取逐渐忘记的的均值)。
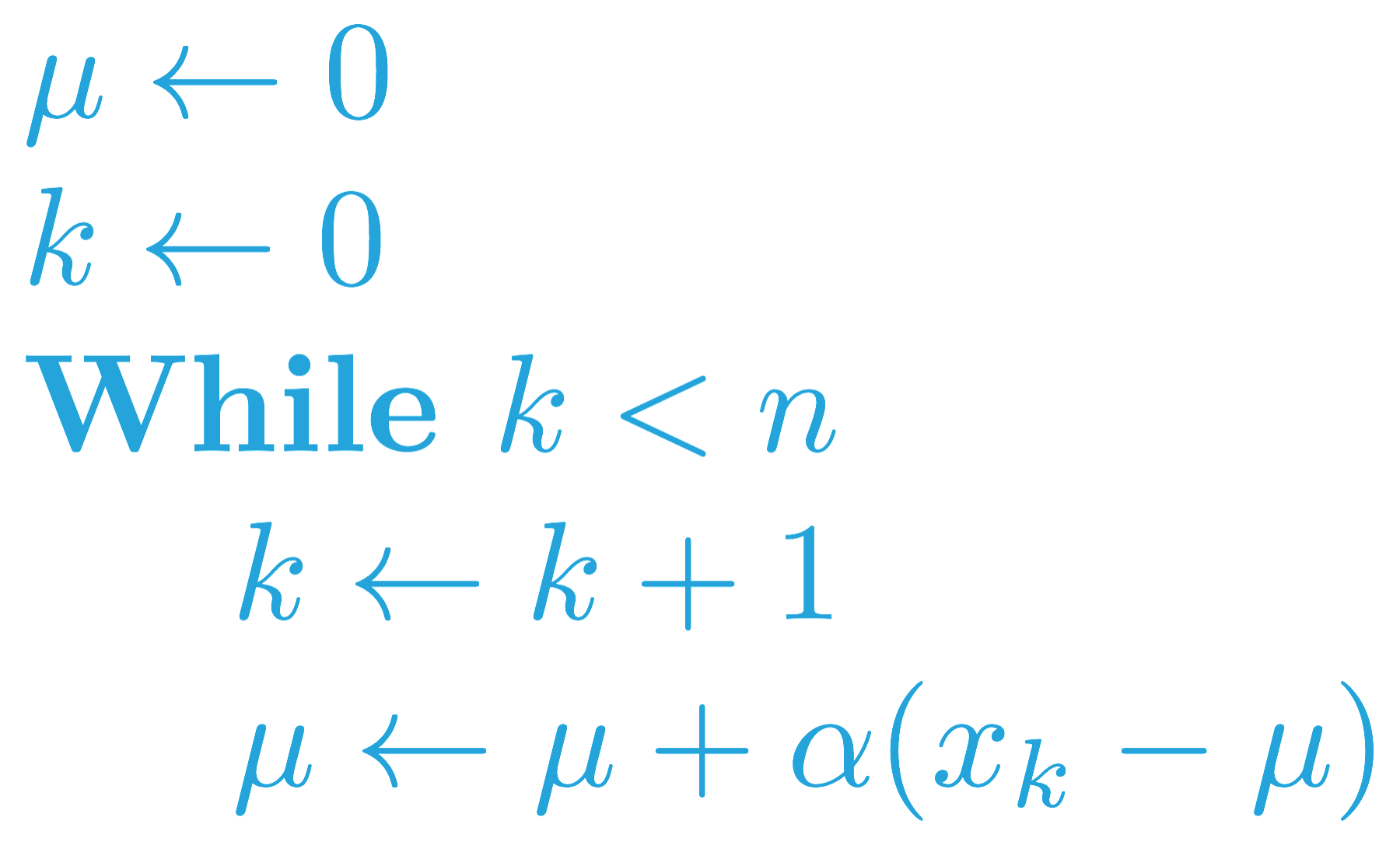
此更改已在下面的 forgetful_mean 函数中实现。该函数接受一系列的数字 x 和步长 alpha 作为输入。返回一个列表 mean_values,其中 mean_values[i] 是第 (i+1) 个估算的状态动作值。
print_results 函数会分析 running_mean 和 forgetful_mean 函数之间的差值。它向两个函数传入相同的 x 值并在 forgetful_mean 函数中测试 alpha 的多个值。
请花时间熟悉下面的代码。然后,点击[测试答案]按钮以执行 print_results 函数。如果你想运行更多的测试以加深理解的话,可以随意更改 x 和 alpha_values 的值。
Start Quiz:
设置 \alpha 的值
注意,forgetful_mean 函数与常量 \alpha MC 控制中的评估步骤紧密相连。你可以在下方找到相关的伪代码。
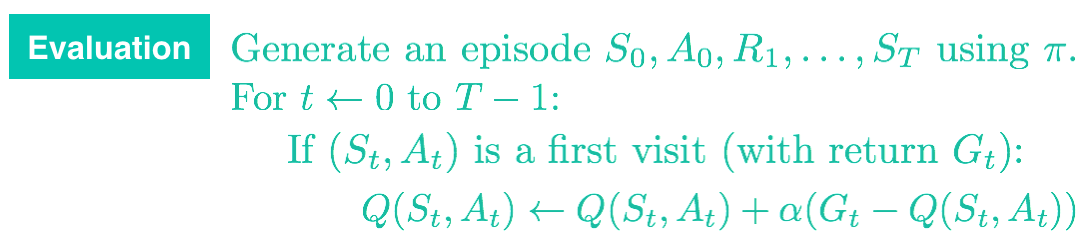
在继续学习下个部分之前,请使用上述代码环境验证在实现常量 \alpha MC 控制时如何设置 \alpha 的值。
你应该始终将 \alpha 的值设为大于 0 并小于等于 1 之间的数字。
- 如果 \alpha=0,则智能体始终不会更新动作值函数估算。
- 如果 \alpha = 1,则每个状态动作对的最终值估算始终等于智能体(访问该对后)最后体验的回报。
如果 \alpha 的值更小,则促使智能体在计算动作值函数估值时考虑更长的回报历史记录。增加 \alpha 的值确保智能体更侧重于最近抽取的回报。
注意,还可以通过稍微如下所示地改写更新步骤验证上述规律:
Q(S_t,A_t) \leftarrow (1-\alpha)Q(S_t,A_t) + \alpha G_t
现在更明显的是,\alpha 会控制信任最近的回报 G_t(而不是通过考虑所有以前的回报得出的估值 Q(S_t,A_t))的程度。
重要事项:在实现常量 \alpha MC 控制时,必须尽量不要将 \alpha 的值设为太接近 1。因为非常大的值可能会导致算法无法收敛于最优策略 \pi_*。但是,也尽量不要将 \alpha 的值设得太小,因为可能会导致智能体的学习速度太慢。在你的实现中,\alpha 的最佳值将很大程度上取决于你的环境,最好通过试错法得出最佳值。